What are the “reasoning papers” in the Year 6 SATs?
The Year 6 maths SATs tests consist of 3 papers: 1 arithmetic and 2 reasoning papers.
It is often the reasoning paper where children can get tripped up and many score significantly higher on their arithmetic papers. It is so common to hear that children are doing well in class but it isn’t reflecting in the scores they achieve on the reasoning papers.
The reasoning paper is designed to assess a child’s ability in fluency, reasoning and problem-solving. This means that they are able to independently select and apply mathematical skills to solve a problem both accurately and in an effective way. Children are always aware of the learning objective in a lesson so they know what math skills to apply when they are solving SATs style word problems. Although they may appear confident with the task, it does not necessarily reflect how well they have retained the concept. During a SATs paper, they are exposed to a range of mathematical areas and need to independently recognise and select the math skills they need to apply. This is why scores in tests may not always accurately reflect a child’s true mathematical ability.
What topics appear in the Reasoning Papers?
Here’s a breakdown of the question contents from 2024. It’s a similar picture each year with Number topics making up the majority of questions.

How can I help my child get better at problem-solving for the reasoning papers?
The simple answer is- lots of experience! Children should have regular opportunities to engage with a variety of problems in different contexts and representations, away from the learning of that objective. In reality, class time is limited and children are often cramming learning in for the 49 objectives of the Year 6 curriculum alone. Time spent on revisiting past topics is crucial but limited time may not allow for this to happen.
What do questions in the reasoning papers look like?
They come in a variety of presentations which is why children need to spend time engaging with them. They need to become used to having to independently apply their skills and familiar with the different styles. Styles of questions are as follows, but not limited to: single and multi-step problems; fill in missing values; ordering & sequencing; inverse; tick one; draw; explain how; true or false; reading graphs; completing tables; visualising; measurement and reading scales.
Single and multi-step problems
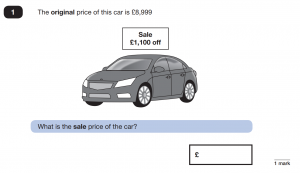
A single step problem requires you to make one calculation. In this example from 2019’s paper 3, we are given the original price and the price to deduct. Children would be expected to recognise that they need to calculate £8999 – £1100 =
In a multi-step problem, there are multiple calculations to make. Paper 3 2019, has a good example. Here children should first calculate 53 x 68 then add this to 105 x 34. This could be written as (53 x 68) + (105 x 34)=

TOP TIP: Sometimes just writing the calculations without an answer can get a mark. If your child can recognise the “number sentence” in the word problem, encourage them to write it even if they can’t solve it or run out of time. Don’t leave it blank if they can avoid it!
Fill in missing values
These types of problems are often linked to inverse or sequencing (see next two examples.) In this example from 2019’s paper 2, you had to fill in all three missing values correctly to obtain 1 mark

Ordering & sequencing
Sequencing questions are common and children are almost always asked to find a prior value in a sequence as well as continuing it. In both sequences below from 2019’s paper 2, the increased value is given. However, in question 8, the increase has two steps, so children need to complete the inverse carefully. To find the inverse of multiply by 2 then add 3 you must “undo” the last step first. Start by subtracting 3 and then divide by 2.


Inverse
Finding the inverse questions assess understanding of which operators are the inverse of each other and how the commutative properties of multiplication do not apply to division.
For 2019’s paper 2, question 6, children can calculate 0.3 ÷ 0.03 = to find the missing value

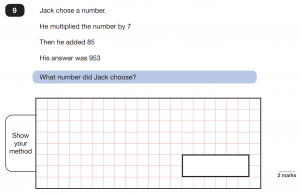
For 2019’s paper 2, question 9, you need to “undo” the last step and work backwards.
1) Start with the answer of 953 2) Subtract 85 3) Divide by 7 to find the original number.
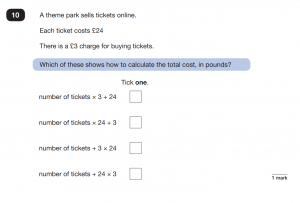
Tick one
You will be given multiple choice answers. Children must check if they are asked to tick one or more answers. There is usually an important instruction in bold. It is common for children to overlook the bold instruction. Both examples are from 2019’s paper 2.

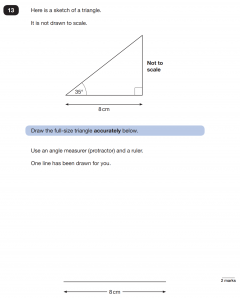
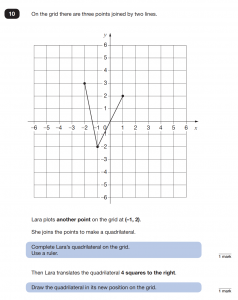
Draw
Questions which require children to draw will be measured using an online ruler. Lines must be straight and there is a very small room for measurement error. Sharp pencils and plenty of practice using a ruler will all help prepare your child for questions like these. Drawing questions are usually geometry related. Below question 13 & 21 are from 2019’s paper 2, while question 10 is from paper 3. Five marks in total are from questions requiring children to draw using their understanding of the properties of 2d shapes.

Explain how & True or false
For these types of questions, your child will be expected to explain their answer. They could be asked to explain how they know something, such as in question 18 from 2019’s paper 2. Or they may be asked to prove or disprove a statement (see question 13 from paper 3 in 2019). The correct use of mathematical vocabulary is crucial here; they may also need to show a calculation to support their explanation.

Reading Graphs
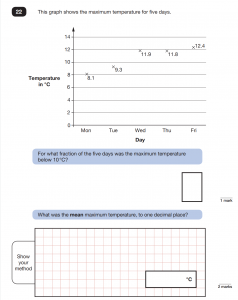
These type of questions require reading graphs and analysing statistics. It could be a line graph, a bar chart or a pie chart but children will be given at least one or two questions which ask them to read the information accurately. One question will usually require being able to read a piece of information from the graph but other questions will need a deeper level of engagement: perhaps comparing more than one piece of data or as in 2019’s paper 2, question 22: finding the average.
Completing tables
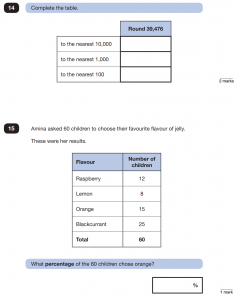
These style of questions are sometimes about reading and engaging with statistics (similar to graph style q’s) as in question 15 from paper 2. They could also be assessing an understanding of how headings work: for example in 2 way tables. Or they could involve testing a different a maths skill – as in question 14- but an understanding of how tables work is required in order to record answers correctly and in the right part on the table.
Visualising
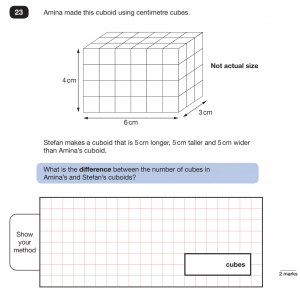
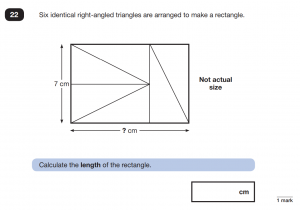
Visualising activities are often related to shapes. Understanding of 3-D shape properties are often presented in these style of questions. In 2019, question 23 from paper 2, is a volume question. You are shown one image, which will help your child visualise the formula for finding the volume, but you are only given the dimensions of the second cuboid which you need to compare with the pictured cuboid. With question 21 and question 22 from 2019’s paper 3 you are shown images from which clues can be derived. The information given, acts like a trail of breadcrumbs, where one clue leads to another and then to another until finally you arrive at the answer. It is a good idea to label images with any clues that can be derived as this will enable further clues to be found.

Measurement
There will be plenty of questions related to measurement. They will usually require some converting of units. Questions could be related to weight, length, volume, time or money. They are often linked to fractions, decimals or percentages and the units of measurements will often be mixed. It is very important to check the answer box to see what unit of measurement the answer must be recorded as. These questions often require more than one calculation to be carried out.
Reading scales
‘Reading scales’ questions often have marked and unmarked intervals and children will be required to figure out the value of the unmarked intervals. Here children will be using their knowledge of fractions and/or decimals. For example, in 2019’s paper 2, question 7, we can see that the mark is halfway between 2l and 3l so children could either write 21/2 l or 2.5l. If the answer box had millilitres written, the children would have to then write 2500ml.

Where can I find good examples of Year 6 SATs reasoning questions?
The Pocket private Tutor Year 6 SATs revision app has a bank of questions on every single learning objective in Year 6. Each objective comes with a comprehensive teaching video with clear explanations and a breakdown of the skills needed. Print the worksheet to complete alongside the videos and you can even view how each objective has appeared in the past SATs papers to get an idea of how it could be presented. The app is available on Google and Apple and you can currently try out 6 lessons for free. At only £9.99 per month, with complete access to the whole of the Year 6 maths curriculum, you can ensure your child has plenty of opportunities to become familiar with reasoning paper style questions and get the best chance of achieving a result they deserve!
You can also sign up to my mailing list and I will send you regular SATs revision resources. To sample an example click here. 
Every revision grid has SATs style questions linked to a Year 6 learning objective and comes complete with the answers. Questions are clearly labelled, so you can identify which National Curriculum objective it is linked to. Use the grid as an opportunity for your child to become familiar with the style of problems they will encounter in the reasoning papers but also to help them highlight areas they are secure in and areas which require further revision.
Join the community of Year 6 Parents
Follow us on Facebook , Instagram or YouTube, where I post regular puzzles, teaching tips, vocabulary definitions and SATs info! I will soon be adding modelled solutions to past SATs papers to our YouTube channel so you can view exactly how a problem could be solved! Subscribe here to find out when this new feature will be live!







Leave a comment
Sign in to post your comment or sign-up if you don't have any account.