What is Ratio?

Ratio and Proportion first appears on the National Curriculum for Mathematics in Year 6 and continues to be a firm part of the Key Stage 3 & 4 curriculum too. It is very much a topic that relates to real life; we use ratio as part of recipes, medicine, and various aspects of building work to name a few! But what does it look like as a topic taught in a maths lesson? Ratio can be linked to but should not be confused with fractions; it has its own distinctive way of representing parts of a whole but like fractions a solid grasp of multiples and factors will make solving problems so much simpler.

Ratio & Fractions
Like fractions, ratio shows parts of a whole. For example, in a pot of purple paint there may be 2 parts blue to 3 parts red. Using fractions, we would say 2/5 of the paint is blue and 3/5 of the paint is red. In ratio we would write is as red to blue is 2:3. We can also simplify ratio as we would with fractions. A ratio of 4:8 can be simplified to 1:2.
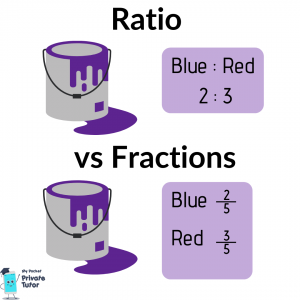

In fractions, the denominator tells us the total number of parts and we use the numerator to compare sizes but only when the denominators are the same. With ratio, the sum of each part tells us the total number of parts, we can simply compare the numbers as they are. For example we can’t compare 2/5 to 3/4 because they don’t have the same denominator. We would have to do some converting so that we would have 8/20 and 15/20 before we can compare the two. With ratio you can compare the numbers each side of the colons without having to do any converting.
We can also use ratio to compare the quantities to each other (the other parts in the whole). Take that same pot of purple paint with 2 parts blue to 3 parts red. We can say that the amount of blue is 2/3 of the amount of red and the amount of red is 3/2 (or 1 ½) the amount of blue.


Keeping things in proportion
I always use the term “scaling” when tackling ratio problems. We may need to scale up or down according to the context but the trick is to identify the scale factor using the given clues then apply that scale factor to the rest of the numbers. Take a look at this past SATs question from Paper 2 in 2022. This explores the learning objective:
- solve problems involving the relative sizes of 2 quantities where missing values can be found by using integer multiplication and division facts
Take a look at an explanation of how to solve here:
Ratio and Recipes
This is a classic example of a math skill that is used in real life. When we use recipes its quite common that it may be designed for more or less people than we are cooking for. If a recipe serves 4 but we only need it for 2, we would halve all of the quantities. If we were cooking for 6 we would need to increase all of the ingredients but we would first need to figure out the scale factor. How mamny times does 4 fit into 6? Or using what we know about ratio and fractions to see that 4:6 (original recipe:desired quantity) = 6/4 = 1 ½. We need to multiply all ingredients by 1 ½.

Ratio and times-tables
Ratio problems are far simpler to solve when you are confident with your times-table facts. Being able to quickly identify multiples or factors will help immensely with reasoning questions. Solving problems usually requires comparing tow numbers and how they link. When you can quickly see that 48 is 12 times 4 you can use this to apply to all other numbers. A solid graps of times tables is key here.
I can help your child get familiar with what Ratio & Proportion questions might like and also some tips on how to work through these problems! There are 4 Ratio & Proportion Learning Obejctives in the Year 6 National Curriculum and I have created lesson tutorials and practice worksheets with SATs style questions in my Ratio & Proportion EBook. It also contains loads of examples of past SATs questions so your child can see the different ways this topic has appeared in actual tests before. Ratio is a key area of maths that will come up a lot from Year 7 onwards, so make sure your child doesn’t miss out on this crucial area of maths that can so often be overlooked or under-taught.







Leave a comment
Sign in to post your comment or sign-up if you don't have any account.